https://docs.google.com/presentation/d/e/2PACX-1vQrLs_76cBJykMiNSGrx55Q9G4dRiW4gred32FMzrFLZCldcpcRe653YLVl3V6zDg/pubembed?start=false&loop=false&delayms=3000
Clustering, ou análise de agrupamentos, é uma técnica essencial de aprendizado não supervisionado que visa particionar um conjunto de dados em grupos (clusters) de instâncias semelhantes, sem utilizar rótulos pré-definidos. Esta disciplina fornece insights sobre estruturas ocultas nos dados, suportando tomada de decisão em diversas áreas como marketing, bioinformática e segurança.
1. Fundamentos de Clustering
- Objetivo: agrupar instâncias de modo que amostras no mesmo cluster sejam mais semelhantes entre si do que em clusters diferentes.
- Diferença para classificação: em clustering não existem rótulos de treino; os grupos emergem dos padrões dos dados.
- Semelhança e distância: medidas comuns incluem distância euclidiana, Manhattan e correlação.
- Tipos de clusters: esféricos, densos, de forma arbitrária e hierárquicos.
2. Algoritmos de Clustering Comuns
2.1 K-Means
- Conceito: particiona dados em k clusters, minimizando a soma das distâncias quadráticas (inércia) entre cada ponto e o centróide do cluster.
- Passos principais:
- Inicializar k centróides (aleatório ou kmeans++).
- Atribuir cada ponto ao centróide mais próximo.
- Recalcular centróides como média dos pontos atribuídos.
- Repetir até convergência ou número máximo de iterações.
- Vantagens: rápido e fácil de implementar; bom para clusters esféricos de tamanho similar.
- Limitações: escolha de k; sensível a outliers; assume forma convexa.
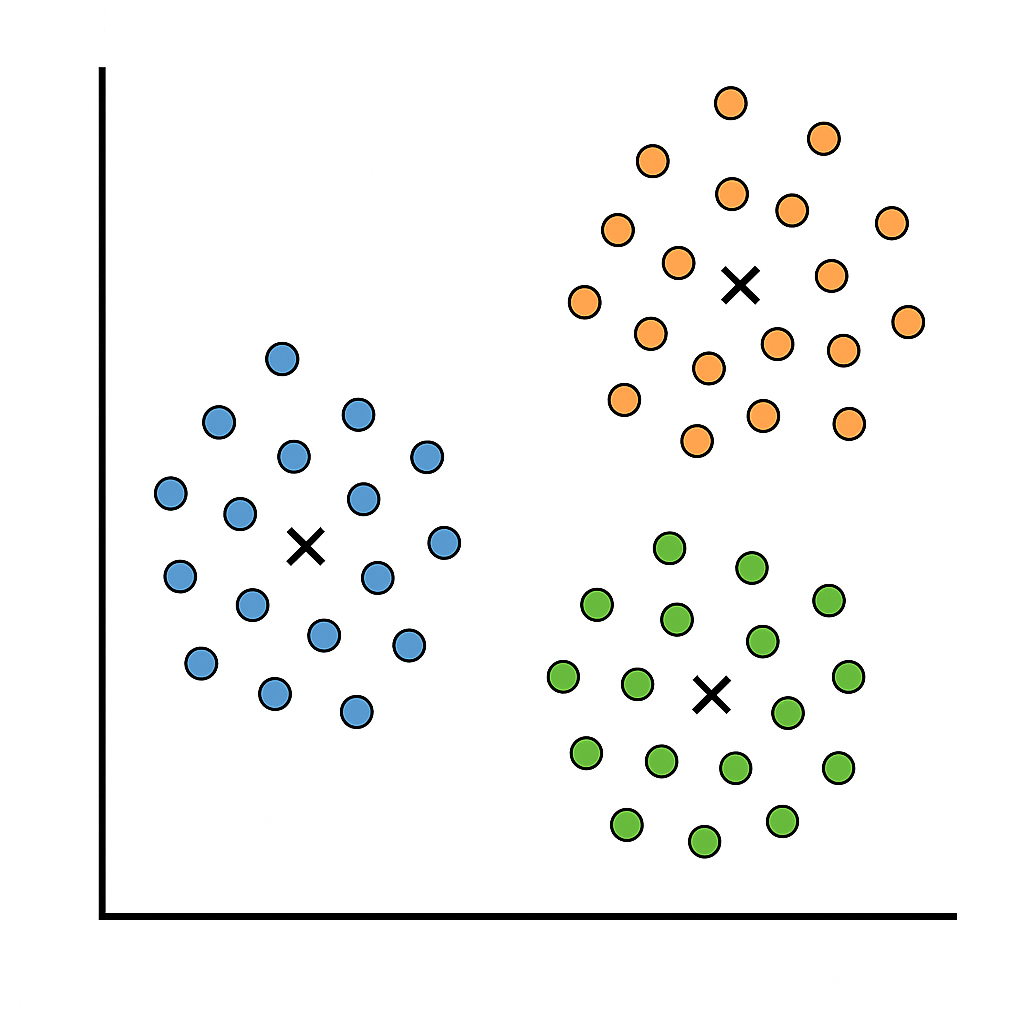
Ilustração de clusters K-means
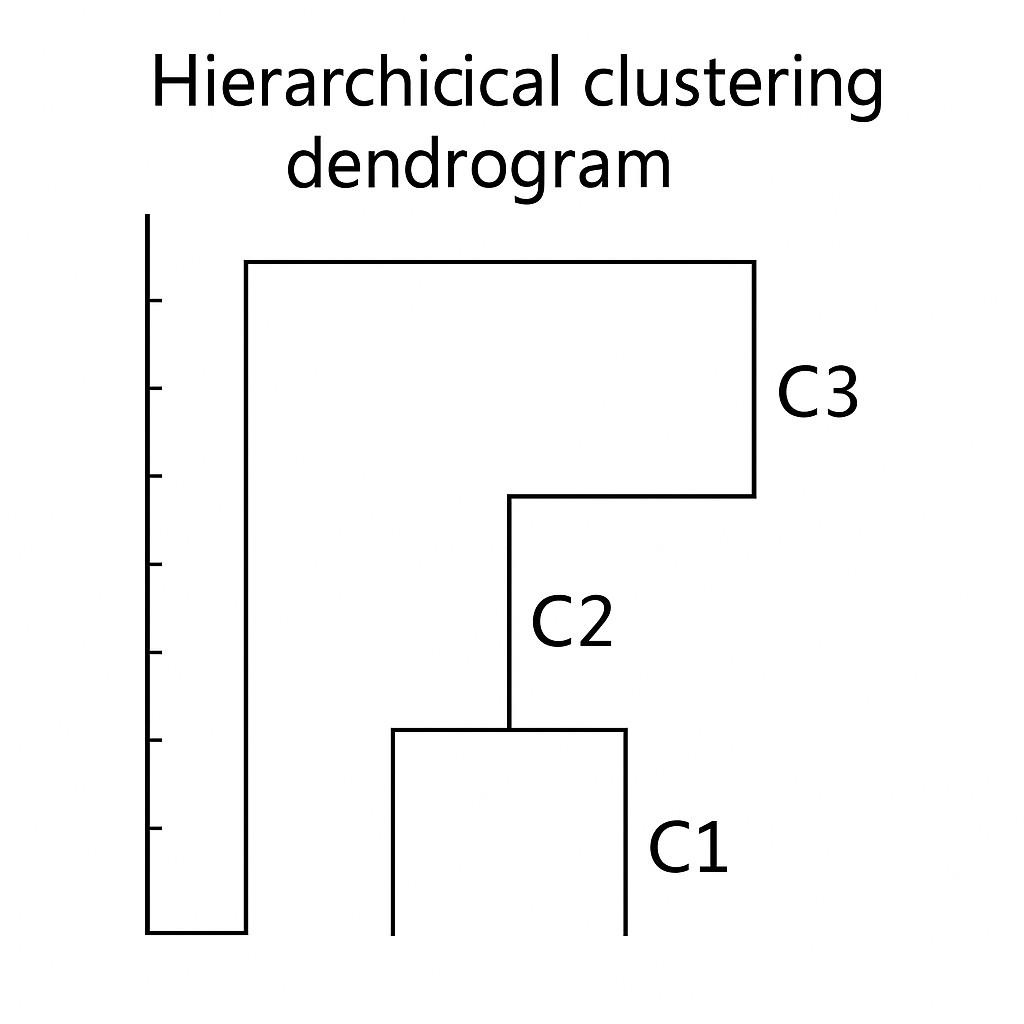
2.2 Clustering Hierárquico
- Abordagens:
- Aglomerativo (bottom-up): cada ponto inicia como cluster; sucessivamente agrupa pares de clusters mais próximos.
- Divisivo (top-down): todo o conjunto inicia em um cluster; recursivamente divide-se clusters até atingir número desejado.
- Variações de ligação: simples, completa e média.
- Dendrograma: representa graficamente o processo de fusão e distância de união.